Refractive index – dependent and independent – axial length measurement in optical biometry for IOL calculation
doi: 10.55342/szemhungarica.2022.159.2.76
Original scientific paper
Summary
Our publication is focused on the potential cost and benefit of using either a refractive index-dependent or an -independent distance measurements in optical biometry for IOL calculation.
Similar to acoustic biometry, where real distances are calculated as a division of the measured length by the respective sound propagation speed, in optical biometry, the denominator is the refractive index of the given medium. Due to simplifying calculation, acoustic biometry uses an averaged propagation speed for the entire bulb. Optical biometry follows this practice dominantly, as distances are corrected with an estimated, cumulative refractive index independently from the respective media. IOL calculation formulas are optimized for such data, supposedly. The question emerged whether the application of distances, calculated with their dedicated refraction indices in formulas are optimized for refraction index-independent data may corrupt results.
Based on the literature, we are going to compare IOL prediction data obtained from these different distance measurement methods.
Összefoglaló
Közleményünk a műlencsetervezés optikai biometriája során alkalmazott távolságmérés törésmutató-függő és -független koncepciójának feltételezett előnyeire, valamint esetleges hátrányira kívánja ráirányítani a figyelmet.Optikai úton történő interferométeres távolságmérés során – hasonlóan az ultrahangalapú méréseknél, hol a hang terjedési sebessége a korrekciós faktor – a mérendő közeg törésmutatója figyelembe veendő. Az egyszerűbb méréstechnika okán azonban az akusztikus biometria egy, átlagos hangterjedési-sebességgel számol. Az optikai biometria gyakorlatában is döntően ez a koncepció érvényesül, tehát a távolságmérés az adott közeg törésmutatójától független, egy, a teljes intraocularis közeg átlagos törésmutatójának becsült átlagos érték figyelembevételével történik. Feltételezhető, hogy a műlencsetervező formulák az így nyert adatokra optimalizáltak. Felmerült bennünk, hogy az adott közeg törésmutatójával, tehát törésmutató-függő módon számolt távolságértékek alkalmazása a feltehetően törésmutatófüggetlen-mérésekre optimalizált formulákban akár hátrányt is jelenthet.
Az elérhető irodalmi adatok alapján kísérletet teszünk a két távolságmérési módszerrel nyert műlencsetervezési eredmények összehasonlítására.
Keywords
optical biometry, refractive index, axial length, formula, prediction error
Kulcsszavak
optikai biometria, törésmutató, tengelyhossz, formula, tervezési hiba
Bevezetés
A műlencsetervezés biometriája során a távolságmérés alapvető fontosságú. Nem csupán azért, mert a tengelyhosszt, mint alapadatot szolgáltatja, ám azért is, mert egyéb paraméterekkel a lencsepozíció becslését teszi lehetővé. Az interferometrián alapuló optikai biometria méréstechnikájában alapelv, hogy a mért távolságot a mérendő közeg törésmutatójával korrigálni kell. Mindez hasonló az akusztikus biometriához, hol a hang közegben való terjedési sebességével egyenesen arányos a mért szakasz valós hossza. Az optikában a törésmutató a fény terjedési sebességével fordítottan arányos mérőszám, tehát az adott intraocularis szakasz műszer által észlelt távolságát osztani kell az adott közeg optikai törésmutatójával. A korrekciót bonyolítja, hogy a műszer által használt hullámhosszra a rendszerint 550 nm-es hullámhosszon kifejezett törésmutatót korrigálni kell, de ökölszabályként elmondható, hogy a valós, „geometriai” távolságot a nyers, „optikai” úthossz és a törésmutató hányadosaként kapjuk meg (3, 7).
Az első műlencsetervező optikai biométernél ez a szempont még nem merült fel, hiszen az interferometriával csupán a tengelyhosszt volt képes mérni, a használt törésmutató pedig egy, az egész bulbus átlagára vonatkoztatott kumulatív érték volt. A későbbiekben, amint az egyes törőközeghatárok mérhetőkké váltak, felmerült annak lehetősége, hogy az adott intraocularis szakaszok hosszai azok törésmutatóival számoltassanak, a tengelyhosszt pedig az egyes szakaszok távolságösszege adja. A tengelyhossz az utóbbi meghatározásának módja azonban az FDA kompatibilitási aggályai miatt meghiúsult, és így ezen úttörő biométernél hibrid távolságmérés került alkalmazásra: a szaruhártya-vastagság, elülsőcsarnok-mélység, lencsevastagság-értékek saját, míg a tengelyhossz kumulatív törésmutatóval számolt (1). Az ezt követően piacra került biométerek is sokáig a tengelyhosszt egyetlen, „átlagos” törésmutatóval számolták, míg piacra került egy, a tengelyhosszt az egyes intraocularis szakaszok saját törésmutatói alapján mért hosszainak összegeként definiáló biométer is.
Az eltérő méréstechnika természetesen eltérő eredményeket is jelent, amely leginkább az átlagtól eltérő nagyságú szemek tengelyhossz-értékeiben mutatkozik meg: a törésmutató-függő hosszmérés átlagnál alacsonyabb bulbushossz mellett magasabb, átlagosnál hosszabb szemeknél viszont kisebb tengelyhosszakat mutat a kumulatív törésmutatóval számoltakkal összevetve (4, 8, 9). Nyilvánvaló, hogy törésmutatófüggő-mérés jelenti a pontosabb tengelyhossz-meghatározást, különösképp, ha az az átlagostól eltérő belső arányú (pl.: rövidebb vagy hosszabb tengelyhosszú) szemeken történik. Elméleti megfontolás alapján egy törésmutató-független (azaz átlagos törésmutatóval számolt) tengelyhosszakra optimalizált formula pontosságára eltérő hatással lehet, ha abban törésmutató-függő tengelyhosszt alkalmazunk. Feltételezhető ugyanis, hogy egy formula, amely az egyes intraocularis szakaszokról, azok arányairól információt nem (pl.: Hoffer-Q, SRK/T), vagy csak részlegesen (Holladay-1, Haigis) hordoz, ott a tengelyhossz törésmutató-függő meghatározása előnyt jelenthet. Olyan formulák esetében azonban, ahol már a lencsevastagság is, azaz minden egyes törőközeg hossza meghatározott, feltételezhető, hogy a formula optimalizálása során a távolságértékek korrekciója megtörtént. Ebben az esetben a mérés során a már korrigált érték formulában történő további módosítása hibát eredményez. (Hasonlóan ahhoz, mint ha a teljes szaruhártyaasztigmia-értéket regressziós tórikus formulában alkalmaznánk.) Mivel a formulák többsége valószínűsíthetően átlagos törésmutató mellett számolt tengelyhosszértékekre optimalizáltak, felmerült bennünk, a törésmutatófüggő-mérések egyes formulákban történő alkalmazhatóságának kérdése. Retrospektív irodalmi áttekintésünkben arra igyekszünk választ adni, hogy az alkalmazott mérési elv miként befolyásolja az egyes formulák prediktív hibáit.
Irodalmi áttekintés
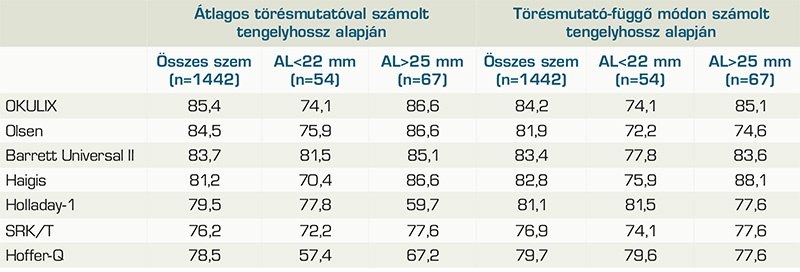
David és Timothy Cooke munkájában a törésmutató-függő és átlagos törésmutatóval számolt tengelyhosszértékekkel kapott prediktív hibákat hasonlították össze különböző formulákban (1). A dedikált törésmutatókkal számolt ACD, LT, valamint az átlagos refrakciós indexszel számolt tengelyhosszak Lenstar LS-900 által számolt értékek voltak, míg a törésmutató-függő tengelyhosszadatok a biométer nyers adataiból, az egyes intraocularis szegmensek saját törésmutatójukkal korrigált értékeinek összegeiként kerültek előállításra, úgy, hogy a teljes vizsgálati csoport átlagában két tengelyhosszérték megegyezett. Ugyanazon típusú műlencse beültetése mellett a formulákhoz tartozó lencsekonstansok mindkét tengelyhosszérték mellett, egyenként optimalizálásra kerültek. A vizsgálatok összesen 1442 szemen történtek, amelyből 54 volt 22 mm alatti, és 67, 25 mm feletti tengelyhosszú. Az átlagos törésmutatóval, valamint törésmutató-függő módon számolt tengelyhosszakkal számolt formulák ±0,5 D prediktív hibatartományának arányait az 1. táblázat mutatja, tengelyhossz szerinti csoportosításban is.
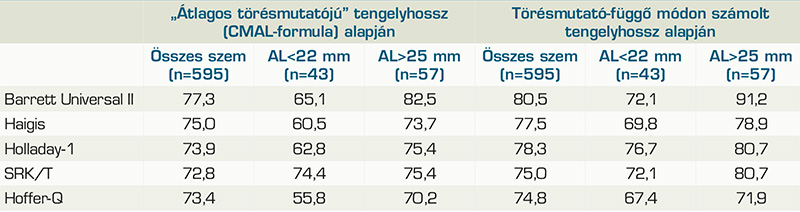
Shammas és munkatársai tükörtanulmányként is felfogható dolgozatában az Argos biométer törésmutató-függő valamint a CMAL (Cooke-modified AL) képlet (2) alapján számolt „átlagos törésmutatójú” tengelyhosszértékeivel alkalmazott formulák prediktív hibáit hasonlították össze (6). A formulákhoz szükséges további szegmensadatok a biométer törésmutató-függő értékei voltak. A különböző módon számolt tengelyhosszak átlaga azonos volt. Egy típusú műlencsét ültettek be, a lencsekonstansok mindkét tengelyhossz mellett optimalizálásra kerültek. A vizsgálatok összesen 595 szemen történtek, amelyből 43 volt 22 mm alatti, és 57, 25 mm feletti tengelyhosszú. A CMAL-formula alapján „átlagos törésmutató” szerint számoltnak becsült, valamint törésmutató-függő módon mért tengelyhosszakkal az egyes formulák ±0,5 D prediktív hibatartományának arányai a 2. táblázatban találhatók.
Mindkét előbbi dolgozatból kiemelendő, a törésmutató-függő tengelyhosszadatok alkalmazása esetén a ±0,5 D prediktív hibatartományba eső szemek arányának növekedése a Holladay-1, Haigis- és Hoffer-Q-formulák esetén, amely főleg az átlagostól eltérő bulbushosszú szemek esetén mutatkozott meg. A Barrett Universal-II-formula a két vizsgálatban eltérően viselkedett: míg Cooke eredményei szerint a törésmutató-függő módon számolt tengelyhosszak, addig Shammas számításai szerint a CMAL-formula alapján becsült „törésmutató-független” tengelyhosszérték csökkentette a formula prediktivitását. Ennek lehetséges magyarázata lehet, hogy a CMAL-képlet jelentősen más hullámhossz-érték alapján lett kifejlesztve, mint amit az Argos biométer használ (2).
Wang és munkatársai közleményében (10), hasonlóan Cooke dolgozatához, Lenstar LS-900 adataiból számolt törésmutató-függő tengelyhosszadatokat nyertek, ezzel, valamint a Lenstar átlagos törésmutatójú tengelyhosszával és törésmutató-függő ACD, LT értékeivel terveztették 4992 szem műlencse értékeit. Az egyes formulák prediktív hibáit a tengelyhossz függvényében ábrázolták. Mivel eltérő típusú lencsék beültetése történt, és ezek konstansait az adott adatbázisra nem optimalizálták, a formulák robusztussága csupán a prediktív hibák görbéinek vízszintestől való eltérésének mértékében értelmezhetők. A Haigis, Holladay-1, SRK-T és Hoffer-Q-formulák esetén a törésmutató-függő tengelyhosszak mellett számolt prediktív hibák tengelyhosszfüggése csekélyebbek bizonyult, míg az Olsen és a Barrett Universal-II-formulák mellett az átlagos törésmutatójú és törésmutató-független mérések tengelyhosszfüggése azonos mértékűnek, bár eltérő irányúnak imponál. Az eredmények hasonlóak az előző két dolgozatéhoz, amennyiben a törésmutató-függő számolás előnye a Haigis, Holladay-1, SRK/T és Hoffer-Q-formulák alkalmazása során tűnik egyértelműen előnyösnek.
Átlagos törésmutatóval, valamint törésmutató-függő módon számoló biométerek összehasonlításakor ezen eltérések már csupán nyomokban vannak jelen: a törésmutató-függő méréstechnika nagyobb bulbushosszak mellett, Haigis-formulával való számolás esetén kisebb prediktív hibát sejtet (11, 12). A Barrett Universal II formula esetén a távolságmérési-módszerrel konzekvens relációba hozható eltérés nem látható (5, 11).
Érdekességként megállapítható, hogy a Hill-RBF online felületén, amennyiben az eszköz típusát a törésmutató-függő módon számoló egységre átállítjuk, annak hatása a műlencsetervezés eredményére még szélsőségesen rövid, illetve hosszú bulbushosszak mellett sincs, mutatva, hogy a mérőeszközök közötti eltérések feloldására csekély figyelem jut. Annak ellenére, hogy csupán a távolságmérés módszereit tekintve is látható, hogy az eltérő számítási elvek (elsősorban az átlagostól eltérő szemek esetén) a mért tengelyhosszak gyakorlati szempontból is figyelembe veendő eltéréseit eredményezik, a formulák prediktív értékét befolyásolják!
Következtetések
Míg szimulációs eredmények alapján a törésmutató-függő hosszmérés a Haigis-formula pontosságának egyértelmű növekedését mutatja, addig a Barrett Universal-II-formula esetén az eredmények már nem egyértelműek, a prediktivitás növekedése mellett felmerül annak lehetősége is, hogy ezzel a módszerrel a Barrett-formula pontossága csökken.
A különböző biométerek eredményeinek összevetése a hosszmérések módszertani eltérésein túl mind a különböző mérések variabilitásában, mind keratométerek különbségei miatt további hibákat tartalmaz. Ennek ellenére a különböző műszerek eredményei, bár csekélyebb mértékben, ám szintén a Haigis-formula prediktivitásának növekedését mutatják törésmutató-függő távolságmérés esetén. Ez törésmutató-függő módszerrel mérő biométer használatakor a Haigis-formula alkalmazása mellett további érvet jelenthet. A modern, lencsevastagságot is figyelembe vevő formulákban a törésmutató-függő tengelyhosszadatok alkalmazásának előnye vagy esetleges hátránya a rendelkezésre álló kisszámú adat miatt nem megítélhető, felvetve ezen kérdés tanulmányozásának szükségességét, esetlegesen a formulák hosszmérési módszert is figyelembe vevő optimalizálásának lehetőségét.
Nyilatkozat
A szerzők kijelentik, hogy az eredeti közlemény megírásával kapcsolatban nem áll fenn velük szemben pénzügyi vagy egyéb lényeges összeütközés, összeférhetetlenségi ok, amely befolyásolhatja a közleményben bemutatott eredményeket, az abból levont következtetéseket vagy azok értelmezését.
Irodalom
1. Cooke DL, Cooke TL. A comparison of two methods to calculate axial length. J Cataract Refract Surg 2019; 45(3): 284–292. https://doi.org/10.1016/j.jcrs.2018.10.039
2. Cooke DL, Cooke TL. Approximating sum-of-segments axial length from a traditional optical low-coherence reflectometry measurement. J Cataract Refract Surg 2019; 45(3): 351–354. https://doi.org/10.1016/j.jcrs.2018.12.026
3. Cooke DL, Cooke TL, Suheimat M, Atchison DA. Standardizing sum-of-segments axial length using refractive index models. Biomed Opt Express 2020; 11(10): 5860–5870. https://doi.org/10.1364/BOE.400471
4. Németh G, Módis L Jr. Ocular measurements of a swept-source biometer: Repeatability data and comparison with an optical low-coherence interferometry biometer. J Cataract Refract Surg 2019; 45(6): 789–797. https://doi.org/10.1016/j.jcrs.2018.12.018
5. Omoto MK, Torii H, Masui S, Ayaki M, Tsubota K, Negishi K. Ocular biometry and refractive outcomes using two swept-source optical coherence tomography-based biometers with segmental or equivalent refractive indices. Sci Rep 2019; 25; 9(1):6557. https://doi.org/10.1038/s41598-019-42968-3
6. Shammas HJ, Shammas MC, Jivrajka RV, Cooke DL, Potvin R. Effects on IOL power calculation and expected clinical outcomes of axial length measurements based on multiple vs. single refractive indices. Clin Ophthalmol 2020; 14: 1511–1519. https://doi.org/10.2147/OPTH.S256851
7. Suheimat M, Verkicharla PK, Mallen EA, Rozema JJ, Atchison DA. Refractive indices used by the Haag-Streit Lenstar to calculate axial biometric dimensions. Ophthalmic Physiol Opt 2015; 35(1): 90–96. https://doi.org/10.1111/opo.12182
8. Szalay L, Tóth-Molnár E. Optikai biométerek összehasonlítása: a hosszmérés, illetve a teljes szaruhártya-törőerőt leíró paraméterek eltérései. Szemészet 2020; 157(4): 280–288.
9. Tamaoki A, Kojima T, Hasegawa A, Yamamoto M, Kaga T, Tanaka K, Ichikawa K. Clinical Evaluation of a new swept-source optical coherence biometer that uses individual refractive indices to measure axial length in cataract patients Ophthalmic Res 2019; 62(1): 11–23. https://doi.org/10.1159/000496690
10. Wang L, Cao D, Weikert MP, Koch DD. Calculation of axial length using a single group refractive index versus using different refractive indices for each ocular segment: theoretical study and refractive outcomes. Ophthalmology 2019; 126(5): 663–670. https://doi.org/10.1016/j.ophtha.2018.12.046
11. Whang WJ, Yoo YS, Kang MJ, Joo CK. Predictive accuracy of partial coherence interferometry and swept-source optical coherence tomography for intraocular lens power calculation. Sci Rep 2018; 8(1): 13732. https://doi.org/10.1038/s41598-018-32246-z
12. Yang CM, Lim, DH, Kim HJ, Chung TY. Comparison of two swept-source optical coherence tomography biometers and a partial coherence interferometer. 2019; 14(10): e0223114. https://doi.org/10.1371/journal.pone.0223114
